# 前端面试题:常用算法
# 1. 时间复杂度
通常使用最差的时间复杂度来衡量一个算法的好坏。
常数时间 O(1) 代表这个操作和数据量没关系,是一个固定时间的操作,比如说四则运算。
对于一个算法来说,可能会计算出如下操作次数 aN + 1,N 代表数据量。那么该算法的时间复杂度就 是 O(N)。因为我们在计算时间复杂度的时候,数据量通常是非常大的,这时候低阶项和常数项可以忽略 不计。
当然可能会出现两个算法都是 O(N) 的时间复杂度,那么对比两个算法的好坏就要通过对比低阶项和常 数项了。
# 2. 位运算
位运算在算法中很有用,速度可以比四则运算快很多。
在学习位运算之前应该知道十进制如何转二进制,二进制如何转十进制。这里说明下简单的计算方式
- 十进制 33 可以看成是 32 + 1 ,并且 33 应该是六位二进制的(因为 33 近似 32 ,而 32 是 2 的五次方,所以是六位),那么 十进制 33 就是 100001 ,只要是 2 的次方,那么就是 1 否则都 为 0 。
- 那么二进制 100001 同理,首位是 2^5 ,末位是 2^0 ,相加得出 33 。
# 3. 左移 <<
左移就是将二进制全部往左移动, 10 在二进制中表示为 1010 ,左移一位后变成 10100 ,转换为十 进制也就是 20 ,所以基本可以把左移看成以下公式 a * (2 ^b)
# 4. 算数右移 >>
算数右移就是将二进制全部往右移动并去除多余的右边, 10 在二进制中表示为 1010 ,右移一位后变 成 101 ,转换为十进制也就是 5 ,所以基本可以把右移看成以下公式 int v = a / (2 ^ b)
右移很好用,比如可以用在二分算法中取中间值
10 << 1 // -> 20
10 >> 1 // -> 5
13 >> 1 // -> 6
# 5. 按位操作
1 )按位与
每一位都为 1 ,结果才为 1
8 | 7 // -> 15
// 1000 | 0111 -> 1111 -> 15
2 )按位或
其中一位为 1 ,结果就是 1
8 | 7 // -> 15 // 1000 | 0111 -> 1111 -> 15
3 )按位异或
每一位都不同,结果才为 1
8 ^ 7 // -> 15
8 ^ 8 // -> 0
// 1000 ^ 0111 -> 1111 -> 15
// 1000 ^ 1000 -> 0000 -> 0
从以上代码中可以发现按位异或就是不进位加法
面试题:两个数不使用四则运算得出和
这道题中可以按位异或,因为按位异或就是不进位加法, 8 ^ 8 = 0 如果进位了,就是 16 了,所以我们只需要将两个数进行异或操作,然后进位。那么也就是说两个二进制都是 1 的位置,左边应该有一个进位 1,所以可以得出以下公式 a + b = (a ^ b) + ((a & b) << 1) ,然后通过迭代的方式模拟加法
function sum(a, b) {
if (a == 0)
return b
if (b == 0)
return a
let newA = a ^ b
let newB = (a & b) << 1
return sum(newA, newB)
}
# 6. 排序
以下两个函数是排序中会用到的通用函数,就不一一写了
function checkArray(array) {
if (!array || array.length <= 2) return
}
function swap(array, left, right) {
let rightValue = array[right]
array[right] = array[left]
array[left] = rightValue
}
# 7. 冒泡排序
冒泡排序的原理如下,从第一个元素开始,把当前元素和下一个索引元素进行比较。如果当前元素大, 那么就交换位置,重复操作直到比较到最后一个元素,那么此时最后一个元素就是该数组中最大的数。 下一轮重复以上操作,但是此时最后一个元素已经是最大数了,所以不需要再比较最后一个元素,只需 要比较到 length 1 的位置。
以下是实现该算法的代码
function bubble(array) {
checkArray(array);
for (let i = array.length - 1; i > 0; i--) {
// 从 0 到 `length - 1` 遍历
for (let j = 0; j < i; j++) {
if (array[j] > array[j + 1]) swap(array, j, j + 1) }
}
return array;
}
该算法的操作次数是一个等差数列n + (n 1) + (n 2) + 1,去掉常数项以后得出时间复杂度是O(n * n)
# 8. 插入排序
插入排序的原理如下。第一个元素默认是已排序元素,取出下一个元素和当前元素比较,如果当前元素大就交换位置。那么此时第一个元素就是当前的最小数,所以下次取出操作从第三个元素开始,向前对 比,重复之前的操作。
以下是实现该算法的代码
function insertion(array) {
checkArray(array);
for (let i = 1; i < array.length; i++) {
for (let j = i - 1; j >= 0 && array[j] > array[j + 1]; j--)
swap(array, j, j + 1);
}
return array;
}
该算法的操作次数是一个等差数列 n + (n 1) + (n 2) + 1 ,去掉常数项以后得出时间复杂度是O(n * n)
# 9. 选择排序
选择排序的原理如下。遍历数组,设置最小值的索引为 0 ,如果取出的值比当前最小值小,就替换最小 值索引,遍历完成后,将第一个元素和最小值索引上的值交换。如上操作后,第一个元素就是数组中的 最小值,下次遍历就可以从索引 1 开始重复上述操作。
以下是实现该算法的代码
function selection(array) {
checkArray(array);
for (let i = 0; i < array.length - 1; i++) {
let minIndex = i;
for (let j = i + 1; j < array.length; j++) {
minIndex = array[j] < array[minIndex] ? j : minIndex;
}
swap(array, i, minIndex);
}
return array;
}
该算法的操作次数是一个等差数列 n + (n 1) + (n 2) + 1 ,去掉常数项以后得出时间复杂度是O(n * n)
# 10. 归并排序
归并排序的原理如下。递归的将数组两两分开直到最多包含两个元素,然后将数组排序合并,最终合并 为排序好的数组。假设我有一组数组 [3, 1, 2, 8, 9, 7, 6],中间数索引是 3 ,先排序数组 [3, 1, 2, 8] 。在这个左边数组上,继续拆分直到变成数组包含两个元素(如果数组长度是奇数的话,会 有一个拆分数组只包含一个元素)。然后排序数组 [3, 1] 和 [2, 8] ,然后再排序数组 [1, 3, 2, 8] ,这样左边数组就排序完成,然后按照以上思路排序右边数组,最后将数组 [1, 2, 3, 8] 和 [6, 7, 9] 排序。
以下是实现该算法的代码
function sort(array) {
checkArray(array);
mergeSort(array, 0, array.length - 1);
return array;
}
function mergeSort(array, left, right) {
// 左右索引相同说明已经只有一个数
if (left === right) return;
// 等同于 `left + (right - left) / 2`
// 相比 `(left + right) / 2` 来说更加安全,不会溢出
// 使用位运算是因为位运算比四则运算快
let mid = parseInt(left + ((right - left) >> 1));
mergeSort(array, left, mid);
mergeSort(array, mid + 1, right);
let help = [];
let i = 0;
let p1 = left;
let p2 = mid + 1;
while (p1 <= mid && p2 <= right) {
help[i++] = array[p1] < array[p2] ? array[p1++] : array[p2++];
}
while (p1 <= mid) {
help[i++] = array[p1++];
}
while (p2 <= right) {
help[i++] = array[p2++];
}
for (let i = 0; i < help.length; i++) {
array[left + i] = help[i];
}
return array;
}
以上算法使用了递归的思想。递归的本质就是压栈,每递归执行一次函数,就将该函数的信息(比如参 数,内部的变量,执行到的行数)压栈,直到遇到终止条件,然后出栈并继续执行函数。对于以上递归 函数的调用轨迹如下
mergeSort(data, 0, 6) // mid = 3
mergeSort(data, 0, 3) // mid = 1
mergeSort(data, 0, 1) // mid = 0
mergeSort(data, 0, 0) // 遇到终止,回退到上一步
mergeSort(data, 1, 1) // 遇到终止,回退到上一步
// 排序 p1 = 0, p2 = mid + 1 = 1
// 回退到 `mergeSort(data, 0, 3)` 执行下一个递归
mergeSort(2, 3) // mid = 2
mergeSort(3, 3) // 遇到终止,回退到上一步
// 排序 p1 = 2, p2 = mid + 1 = 3
// 回退到 `mergeSort(data, 0, 3)` 执行合并逻辑
// 排序 p1 = 0, p2 = mid + 1 = 2
// 执行完毕回退
// 左边数组排序完毕,右边也是如上轨迹
该算法的操作次数是可以这样计算:递归了两次,每次数据量是数组的一半,并且最后把整个数组迭代 了一次,所以得出表达式 2T(N / 2) + T(N) (T 代表时间,N 代表数据量)。根据该表达式可以套用 公式 得出时间复杂度为 O(N * logN)
# 11. 快排
快排的原理如下。随机选取一个数组中的值作为基准值,从左至右取值与基准值对比大小。比基准值小 的放数组左边,大的放右边,对比完成后将基准值和第一个比基准值大的值交换位置。然后将数组以基 准值的位置分为两部分,继续递归以上操作。
以下是实现该算法的代码
function sort(array) {
checkArray(array);
quickSort(array, 0, array.length - 1);
return array;
}
function quickSort(array, left, right) {
if (left < right) {
swap(array, , right)
// 随机取值,然后和末尾交换,这样做比固定取一个位置的复杂度略低
let indexs = part(array, parseInt(Math.random() * (right - left + 1)) + left, right);
quickSort(array, left, indexs[0]);
quickSort(array, indexs[1] + 1, right);
}
}
function part(array, left, right) {
let less = left - 1;
let more = right;
while (left < more) {
if (array[left] < array[right]) {
// 当前值比基准值小,`less` 和 `left` 都加一
++less;
++left;
} else if (array[left] > array[right]) {
// 当前值比基准值大,将当前值和右边的值交换
// 并且不改变 `left`,因为当前换过来的值还没有判断过大小
swap(array, --more, left);
} else {
// 和基准值相同,只移动下标
left++;
}
}
// 将基准值和比基准值大的第一个值交换位置
// 这样数组就变成 `[比基准值小, 基准值, 比基准值大]`
swap(array, right, more);
return [less, more];
}
该算法的复杂度和归并排序是相同的,但是额外空间复杂度比归并排序少,只需 O(logN),并且相比归并排序来说,所需的常数时间也更少。
面试题
1 )Sort Colors (颜色排序):
题目需要我们将 [2,0,2,1,1,0] 排序成 [0,0,1,1,2,2] ,这个问题就可以使用三路快排的思想。
以下是代码实现
var sortColors = function(nums) {
let left = -1;
let right = nums.length;
let i = 0;
// 下标如果遇到 right,说明已经排序完成
while (i < right) {
if (nums[i] == 0) {
swap(nums, i++, ++left);
} else if (nums[i] == 1) {
i++;
} else {
swap(nums, i, --right);
}
}
};
2 )Kth Largest Element in an Array (数组中第k大的数字):
题目需要找出数组中第 K 大的元素,这问题也可以使用快排的思路。并且因为是找出第 K 大元素,所以 在分离数组的过程中,可以找出需要的元素在哪边,然后只需要排序相应的一边数组就好。
以下是代码实现
var findKthLargest = function(nums, k) {
let l = 0
let r = nums.length - 1
// 得出第 K 大元素的索引位置
k = nums.length - k
while (l < r) {
// 分离数组后获得比基准树大的第一个元素索引
let index = part(nums, l, r)
// 判断该索引和 k 的大小
if (index < k) {
l = index + 1
} else if (index > k) {
r = index - 1
} else {
break
}
}
return nums[k]
};
function part(array, left, right) {
let less = left - 1;
let more = right;
while (left < more) {
if (array[left] < array[right]) {
++less;
++left;
} else if (array[left] > array[right]) {
swap(array, --more, left);
} else {
left++;
}
}
swap(array, right, more);
return more;
}
# 12. 堆排序
堆排序利用了二叉堆的特性来做,二叉堆通常用数组表示,并且二叉堆是一颗完全二叉树(所有叶节点(最底层的节点)都是从左往右顺序排序,并且其他层的节点都是满的)。二叉堆又分为大根堆与小根堆。
- 大根堆是某个节点的所有子节点的值都比他小
- 小根堆是某个节点的所有子节点的值都比他大
堆排序的原理就是组成一个大根堆或者小根堆。以小根堆为例,某个节点的左边子节点索引是 i * 2 + 1 ,右边是 i * 2 + 2,父节点是 (i 1) /2。
- 首先遍历数组,判断该节点的父节点是否比他小,如果小就交换位置并继续判断,直到他的父节点比他大
- 重新以上操作 1 ,直到数组首位是最大值
- 然后将首位和末尾交换位置并将数组长度减一,表示数组末尾已是最大值,不需要再比较大小
- 对比左右节点哪个大,然后记住大的节点的索引并且和父节点对比大小,如果子节点大就交换位置
- 重复以上操作 3 4 直到整个数组都是大根堆。
以下是实现该算法的代码
function heap(array) {
checkArray(array);
// 将最大值交换到首位
for (let i = 0; i < array.length; i++) {
heapInsert(array, i);
}
let size = array.length;
// 交换首位和末尾
swap(array, 0, --size);
while (size > 0) {
heapify(array, 0, size);
swap(array, 0, --size);
}
return array;
}
function heapInsert(array, index) {
// 如果当前节点比父节点大,就交换
while (array[index] > array[parseInt((index - 1) / 2)]) {
swap(array, index, parseInt((index - 1) / 2));
// 将索引变成父节点
index = parseInt((index - 1) / 2);
}
}
function heapify(array, index, size) {
let left = index * 2 + 1;
while (left < size) {
// 判断左右节点大小
let largest = left + 1 < size && array[left] < array[left + 1] ? left + 1 : left;
// 判断子节点和父节点大小
largest = array[index] < array[largest] ? largest : index;
if (largest === index) break;
swap(array, index, largest);
index = largest;
left = index * 2 + 1;
}
}
以上代码实现了小根堆,如果需要实现大根堆,只需要把节点对比反一下就好。 该算法的复杂度是 O(logN)
# 13. 系统自带排序实现
每个语言的排序内部实现都是不同的。
对于 JS 来说,数组长度大于 10 会采用快排,否则使用插入排序。选择插入排序是因为虽然时间复杂度很差,但是在数据量很小的情况下和 O(N * logN)相差无几,然而插入排序需要的常数时间很小,所 以相对别的排序来说更快。
对于 Java 来说,还会考虑内部的元素的类型。对于存储对象的数组来说,会采用稳定性好的算法。稳定 性的意思就是对于相同值来说,相对顺序不能改变。
# 14. 链表
面试题:反转单向链表
题目需要将一个单向链表反转。思路很简单,使用三个变量分别表示当前节点和当前节点的前后节点, 虽然这题很简单,但是却是一道面试常考题
以下是实现该算法的代码
var reverseList = function(head) {
// 判断下变量边界问题
if (!head || !head.next) return head
// 初始设置为空,因为第一个节点反转后就是尾部,尾部节点指向 null
let pre = null
let current = head
let next
// 判断当前节点是否为空
// 不为空就先获取当前节点的下一节点
// 然后把当前节点的 next 设为上一个节点
// 然后把 current 设为下一个节点,pre 设为当前节点
while(current) {
next = current.next
current.next = pre
pre = current
current = next
}
return pre
};
# 15. 二叉树的先序,中序,后序遍历
先序遍历表示先访问根节点,然后访问左节点,最后访问右节点。
中序遍历表示先访问左节点,然后访问根节点,最后访问右节点。
后序遍历表示先访问左节点,然后访问右节点,最后访问根节点。
# 16. 递归实现
递归实现相当简单,代码如下
function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
var traversal = function(root) {
if (root) {
// 先序
console.log(root);
traversal(root.left);
// 中序
// console.log(root);
traversal(root.right);
// 后序
// console.log(root);
}
};
对于递归的实现来说,只需要理解每个节点都会被访问三次就明白为什么这样实现了。
# 17. 非递归实现
非递归实现使用了栈的结构,通过栈的先进后出模拟递归实现。
以下是先序遍历代码实现
function pre(root) {
if (root) {
let stack = [];
// 先将根节点 push
stack.push(root);
// 判断栈中是否为空
while (stack.length > 0) {
// 弹出栈顶元素
root = stack.pop();
console.log(root);
// 因为先序遍历是先左后右,栈是先进后出结构
// 所以先 push 右边再 push 左边
if (root.right) {
stack.push(root.right);
}
if (root.left) {
stack.push(root.left);
}
}
}
}
以下是中序遍历代码实现
function mid(root) {
if (root) {
let stack = [];
// 中序遍历是先左再根最后右
// 所以首先应该先把最左边节点遍历到底依次 push 进栈
// 当左边没有节点时,就打印栈顶元素,然后寻找右节点
// 对于最左边的叶节点来说,可以把它看成是两个 null 节点的父节点
// 左边打印不出东西就把父节点拿出来打印,然后再看右节点
while (stack.length > 0 || root) {
if (root) {
stack.push(root);
root = root.left;
} else {
root = stack.pop();
console.log(root);
root = root.right;
}
}
}
}
以下是后序遍历代码实现,该代码使用了两个栈来实现遍历,相比一个栈的遍历来说要容易理解很多
function pos(root) {
if (root) {
let stack1 = [];
let stack2 = [];
// 后序遍历是先左再右最后根
// 所以对于一个栈来说,应该先 push 根节点
// 然后 push 右节点,最后 push 左节点
stack1.push(root);
while (stack1.length > 0) {
root = stack1.pop();
stack2.push(root);
if (root.left) {
stack1.push(root.left);
}
if (root.right) {
stack1.push(root.right);
}
}
while (stack2.length > 0) {
console.log(s2.pop());
}
}
}
# 18. 中序遍历的前驱后继节点
实现这个算法的前提是节点有一个 parent 的指针指向父节点,根节点指向 null 。
1 )前驱节点
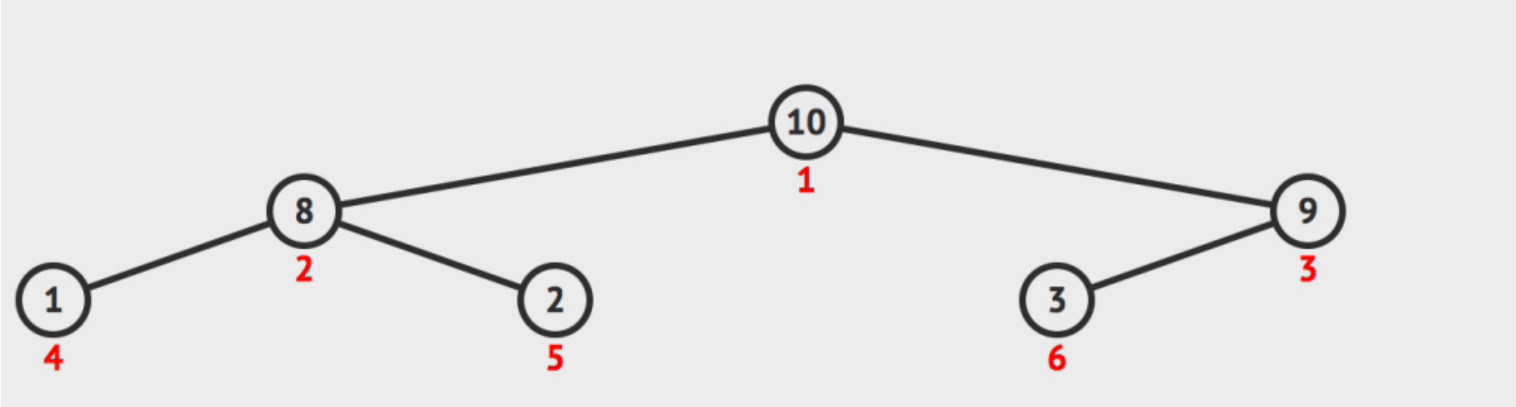
对于节点 2 来说,他的前驱节点就是 4 ,按照中序遍历原则,可以得出以下结论
( 1 )如果选取的节点的左节点不为空,就找该左节点最右的节点。对于节点 1 来说,他有左节点 2 ,那么节点 2 的最右节点就是 5
( 2 )如果左节点为空,且目标节点是父节点的右节点,那么前驱节点为父节点。对于节点 5 来说,没 有左节点,且是节点 2 的右节点,所以节点 2 是前驱节点
( 3 )如果左节点为空,且目标节点是父节点的左节点,向上寻找到第一个是父节点的右节点的节点。对 于节点 6 来说,没有左节点,且是节点 3 的左节点,所以向上寻找到节点 1 ,发现节点 3 是节点 1 的右节点,所以节点 1 是节点 6 的前驱节点
以下是算法实现
function predecessor(node) {
if (!node) return
// 结论 1
if (node.left) {
return getRight(node.left)
} else {
let parent = node.parent
// 结论 2 3 的判断
while(parent && parent.right === node) {
node = parent parent = node.parent
}
return parent
}
}
function getRight(node) {
if (!node) return
node = node.right
while(node) node = node.right
return node
}
2 )后继节点
对于节点 2 来说,他的后继节点就是 5 ,按照中序遍历原则,可以得出以下结论
( 1 )如果有右节点,就找到该右节点的最左节点。对于节点 1 来说,他有右节点 3 ,那么节点 3 的最左节点就是 6
( 2 )如果没有右节点,就向上遍历直到找到一个节点是父节点的左节点。对于节点 5 来说,没有右节点,就向上寻找到节点 2 ,该节点是父节点 1 的左节点,所以节点 1 是后继节点
以下是算法实现
function successor(node) {
if (!node) return
// 结论 1
if (node.right) {
return getLeft(node.right)
} else {
// 结论 2
let parent = node.parent
// 判断 parent 为空
while(parent && parent.left === node) {
node = parent parent = node.parent
}
return parent
}
}
function getLeft(node) {
if (!node) return
node = node.left
while(node) node = node.left
return node
}
# 19. 树的深度
面试题:树的最大深度:
题目需要求出一颗二叉树的最大深度
以下是算法实现
var maxDepth = function(root) {
if (!root) return 0
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1
};
对于该递归函数可以这样理解:一旦没有找到节点就会返回 0 ,每弹出一次递归函数就会加一,树有三层就会得到 3 。
# 20. 动态规划
动态规划背后的基本思想非常简单。就是将一个问题拆分为子问题,一般来说这些子问题都是非常相似 的,那么我们可以通过只解决一次每个子问题来达到减少计算量的目的。
一旦得出每个子问题的解,就存储该结果以便下次使用。
# 21. 斐波那契数列
斐波那契数列就是从 0 和 1 开始,后面的数都是前两个数之和
0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 ,89....
那么显然易见,我们可以通过递归的方式来完成求解斐波那契数列
function fib(n) {
if (n < 2 && n >= 0) return n
return fib(n - 1) + fib(n - 2)
}
fib(10)
以上代码已经可以完美的解决问题。但是以上解法却存在很严重的性能问题,当 n 越大的时候,需要的 时间是指数增长的,这时候就可以通过动态规划来解决这个问题。 动态规划的本质其实就是两点
( 1 )自底向上分解子问题
( 2 )通过变量存储已经计算过的解
根据上面两点,我们的斐波那契数列的动态规划思路也就出来了
( 1 )斐波那契数列从 0 和 1 开始,那么这就是这个子问题的最底层
( 2 )通过数组来存储每一位所对应的斐波那契数列的值
# 22. 0-1背包问题
该问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。每个问题只能放入至多一次。
假设我们有以下物品
| 物品ID / 重量 | 价值 |
|---|---|
| 1 | 3 |
| 2 | 7 |
| 3 | 12 |
对于一个总容量为 5 的背包来说,我们可以放入重量 2 和 3 的物品来达到背包内的物品总价值最高。
对于这个问题来说,子问题就两个,分别是放物品和不放物品,可以通过以下表格来理解子问题
| 物品 ID / 剩余容量 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 1 | 0 | 3 | 3 | 3 | 3 | 3 |
| 2 | 0 | 3 | 7 | 10 | 10 | 10 |
| 3 | 0 | 3 | 7 | 12 | 15 | 19 |
直接来分析能放三种物品的情况,也就是最后一行
- 当容量少于 3 时,只取上一行对应的数据,因为当前容量不能容纳物品 3
- 当容量 为 3 时,考虑两种情况,分别为放入物品 3 和不放物品 3
- 不放物品 3 的情况下,总价值为 10
- 放入物品 3 的情况下,总价值为 12 ,所以应该放入物品 3
- 当容量 为 4 时,考虑两种情况,分别为放入物品 3 和不放物品 3
- 不放物品 3 的情况下,总价值为 10
- 放入物品 3 的情况下,和放入物品 1 的价值相加,得出总价值为 15 ,所以应该放入物品 3
- 当容量 为 5 时,考虑两种情况,分别为放入物品 3 和不放物品 3
- 不放物品 3 的情况下,总价值为 10
- 放入物品 3 的情况下,和放入物品 2 的价值相加,得出总价值为 19 ,所以应该放入物品 3
以下代码对照上表更容易理解
/**
* @param {*} w 物品重量
* @param {*} v 物品价值
* @param {*} C 总容量
* @returns
*/
function knapsack(w, v, C) {
let length = w.length
if (length === 0) return 0
// 对照表格,生成的二维数组,第一维代表物品,第二维代表背包剩余容量
// 第二维中的元素代表背包物品总价值
let array = new Array(length).fill(new Array(C + 1).fill(null))
// 完成底部子问题的解
for (let i = 0; i <= C; i++) {
// 对照表格第一行, array[0] 代表物品 1
// i 代表剩余总容量
// 当剩余总容量大于物品 1 的重量时,记录下背包物品总价值,否则价值为 0
array[0][i] = i >= w[0] ? v[0] : 0 }
// 自底向上开始解决子问题,从物品 2 开始
for (let i = 1; i < length; i++) {
for (let j = 0; j <= C; j++) {
// 这里求解子问题,分别为不放当前物品和放当前物品
// 先求不放当前物品的背包总价值,这里的值也就是对应表格中上一行对应的值
array[i][j] = array[i - 1][j]
// 判断当前剩余容量是否可以放入当前物品
if (j >= w[i]) {
// 可以放入的话,就比大小
// 放入当前物品和不放入当前物品,哪个背包总价值大
array[i][j] = Math.max(array[i][j], v[i] + array[i - 1][j - w[i]])
}
}
}
return array[length - 1][C]
}
# 23. 最长递增子序列
最长递增子序列意思是在一组数字中,找出最长一串递增的数字,比如
0, 3, 4, 17, 2, 8, 6, 10
对于以上这串数字来说,最长递增子序列就是 0, 3, 4, 8, 10,可以通过以下表格更清晰的理解
| 数字 | 0 | 3 | 4 | 17 | 2 | 8 | 6 | 10 |
|---|---|---|---|---|---|---|---|---|
| 长度 | 1 | 2 | 3 | 4 | 2 | 4 | 4 | 5 |
通过以上表格可以很清晰的发现一个规律,找出刚好比当前数字小的数,并且在小的数组成的长度基础上加一。
这个问题的动态思路解法很简单,直接上代码
function lis(n) {
if (n.length === 0) return 0
// 创建一个和参数相同大小的数组,并填充值为 1
let array = new Array(n.length).fill(1)
// 从索引 1 开始遍历,因为数组已经所有都填充为 1 了
for (let i = 1; i < n.length; i++) {
// 从索引 0 遍历到 i
// 判断索引 i 上的值是否大于之前的值
for (let j = 0; j < i; j++) {
if (n[i] > n[j]) {
array[i] = Math.max(array[i], 1 + array[j])
}
}
}
let res = 1
for (let i = 0; i < array.length; i++) {
res = Math.max(res, array[i])
}
return res
}
# 24. 字符串相关
在字符串相关算法中,Trie 树可以解决解决很多问题,同时具备良好的空间和时间复杂度,比如以下问题
- 词频统计
- 前缀匹配